What makes problems difficult?

 

Psychologists have been better at measuring intelligence than explaining how they do so. “The indifference of the indicator” is all very well, but this dictum has been met with public indifference and incomprehension. This is because psychometricians keep saying that intelligence matters, but then put their foot in it by saying “but how you test it doesn’t matter”. Technically, this is correct: it does not matter precisely what the test is, so long as it has sufficient difficulty to stretch minds and grade them. In that sense the actual indicator of intelligence is a matter of indifference, but only so long as it has the necessary psychometric properties.

I try to get round this problem of understanding by giving the example of digit span: remembering digits forward is easy (and only weakly predictive of general ability) but remembering digits backwards is harder (and more strongly predictive of general ability). In that difference lies the essence of difficulty.

http://drjamesthompson.blogspot.co.uk/2014/03/digit-span-modest-little-bombshell.html

It then gets rather technical. Some tests are good indicators at the lower end of ability, others at the higher end. They all have characteristics and quirks. Hence the reification of intelligence test results into g which satisfies most researchers but bemuses the general public.

Compare this with the forced expiratory volume test.

Forced expiratory volume (FEV) measures how much air a person can exhale during a forced breath. The amount of air exhaled may be measured during the first (FEV1), second (FEV2), and/or third seconds (FEV3) of the forced breath. Forced vital capacity (FVC) is the total amount of air exhaled during the FEV test.

Neat, isn’t it? (You can then study whether 30 mins of aerobic exercise over 8 weeks raises the volumes. It does, a bit.) Can psychometrics define an intelligence measure in as simple a way?

Diego Blum, Heinz Holling, Maria Silvia Galibert, Boris Forthmann.  Task difficulty prediction of figural analogies. doi:10.1016/j.intell.2016.03.001

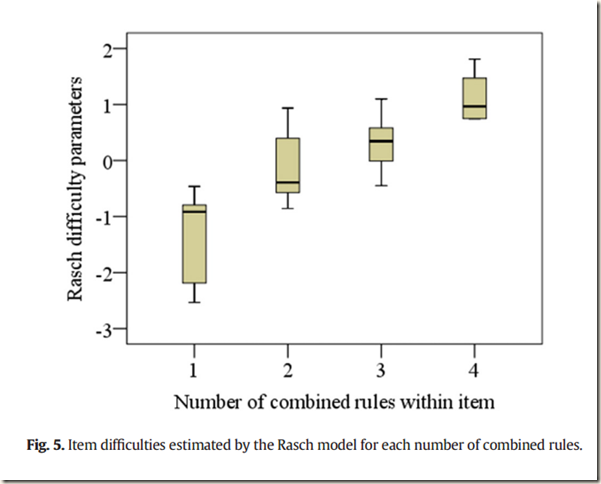
The purpose of this psychometric study is to explain performance on cognitive tasks pertaining Analogical Reasoning that were taken into consideration during the construction of a Test of Figural Analogies. For this purpose, a general Linear Logistic Test Model (LLTM) was mainly used for data analysis. A 30-itemed Test of Figural Analogies was administered to a sample of 422 students from Argentina, and eight of these items were administered along with a Matrices Test to 84 participants mostly from Germany. Women represented 77% and 76% of each respective sample. Indicators of validity and reliability show acceptable results. Item difficulties can be predicted by a set of nine Cognitive Operations to a satisfactory extent, as the Pearson correlation between the Rasch model and the LLTM item difficulty parameters r = .89, the mean prediction error is slightly different between the two models, and there is an overall effect of the number of combined rules on item difficulty (F_(3,23) = 15.16, p < .001) with an effect sizeη² = .66 (large effect). Results suggest that almost all rotation rules are highly influential on item difficulty. (my emphasis).

 

Figural matrices are a good test of intelligence. Raven dreamed his up from logical principles, using patterns he had seen on pottery in the British Museum. His test works very well, even though one difficult item among the 60 is placed a little too early in the B sequence. Incidentally, to my mind this placing error is one of the proofs that the test is reasonably culture fair, in that all racial groups find it difficult, without having to confer across continents about it.

Tests of this sort are known as the A:B::C:D analogies (A is to B as C is to D). When a problem is based on finding the missing element D of the analogy (I.e., A:B::C:?), then C:D becomes the target analog and A:B becomes the source analog. What needs to be extrapolated from one domain to the other is the compound of structural relations that binds these two entities, and not just superficial data (Gentner, 1983). The basic problem A:B::C:? can be applied to different types of contents, namely: verbal, pictorial and figural (Wolf Nelson & Gillespie, 1991).

How does one describe the difficulty level of each item? Mulholland, Pellegrino, and Glaser (1980) studied the causes of item difficulty in geometric analogy problems, and concluded that the number of item elements, as well as the number of transformations, had a significant effect on error rates.

These authors decided to build a test with designed levels of item difficulty, and chose to keep the same standard figures in all items, so as to reduce surface complexity and concentrate on underlying operational differences between items. They used 9 main rules to build the items, rotating the figures by 45, 90 and 180 degrees, using X and Y axis reflections, line subtractions and dot movements. You can call this: “How to build your own IQ test” and the supplementary material shows you how to do this. Note that certain rule combinations lead to some imprecisions and, therefore, the process of rule-based item generation should not be considered a pure-mechanical procedure. As a consequence, the authors have further explanations about their design guidelines which need to be understood

 

 

Based on the data provided in Table 2, specific rule-based contributions to item difficulty can be interpreted. The short clockwise main shape rotation, the subtraction and the dot movement rules make some contributions in this regard. Most interestingly, the best predictors of item difficulty are all the other rotation rules (I.e., both counter clockwise rotations, both long rotations, and the short clockwise trapezium rotation), followed by the reflection rule. Special mention must be given to the long clockwise trapezium rotation, which has the biggest influence on item difficulty. In other words, people found it most difficult to manipulate rotations during task resolution. In fact, the two easiest items according to the Rasch model (items 2 and 4) do not comprise rotation rules, nor does item 25 which is the 7th easiest item. Also, combining rules within a single item has an impact on item difficulty by itself, since both the ANOVA results and the Box Plot show that the higher the number of combined rules, the greater the item difficulties.

I am aware that some of this has been done before, if only because I attended conferences years ago showing that an intelligence test could be constructed out of general principles of learning, and that it had good predictive value.

I think that this is a good paper which should be mentioned whenever critics assume that test material is arbitrary and unrepresentative in some way. This work establishes that rules of design complexity are strongly associated with the ease or difficulty human subjects experience when they solve problems.

One fly in the ointment: it seems that psychology is now 76% a girly subject and women are less good at mental rotation of shapes, so it might be good to check this with boys studying something other than psychology.

The authors found that this test works well at low as well as high levels of ability, which is particularly useful.

A high positive correlation (r = .89) reveals that item difficulties are strongly associated with the predicted difficulties of each rule, and these item difficulties remain practically unchanged in a further study.

By wary of comparison only, the test-retest correlation of the Wechsler after 6  months is 0.93, so the above correlation of 0.89 is a very strong endorsement of the design principles of the test created by the authors.

Perhaps we have taken a step towards finding out what makes problems difficult.

Take a closer look at the paper here:

https://drive.google.com/file/d/0B3c4TxciNeJZcWZiUmpfRm50VlE/view?usp=sharing