A reader (Panjoomby) commenting on the previous post asked a question about the 0.81 correlation between intelligence and scholastic attainment, commending Deary et al. for their methods, so I thought I would pick out the key part of the paper for illustrative purposes.
The authors did a factor analysis of the Cognitive Assessment Test (CAT) which is shown in the structured equation below as F1 and a factor analysis of the most commonly taken GCSE exams which is shown as F2. The correlation between the two is 0.81
This method, described in more detail in the text below is the best way to present the results. As other readers have commented, this is a very strong correlation, unusual in social science research.
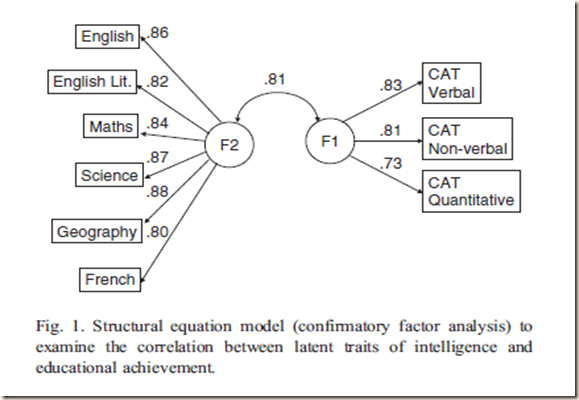

Contra Panjoomby, the .81 correlation is not analogous to a canonical correlation. There was no attempt to maximize the correlation between the two factors. Rather, the correlation is an empirical finding indicating the degree of similarity between two factors derived from completely different sets of variables. Using this method, the correlation could have been anything from -1 to +1, but it was .81.
ReplyDeletethank you - understood!
ReplyDeleteAm I correct in thinking that what Deary et al. have done is roughly the reverse of what Spearman did in 1904 -- i.e., deriving g from the observed performance of students?
ReplyDeleteAlthough of course Deary et al. were not "deriving" academic test scores from more g-loaded test scores.
DeleteBoth Spearman and Deary have been doing the same thing: taking a range of tests and deriving the latent factors, in the Deary's case the latent factor of cognitive abilities tests (school far) and the latent factor of scholastic tests (school near).
ReplyDeleteinteresting they found a single achievement factor that accounted for 71.8% of the variance - i guess they stacked the tables that way using PAF (?) -- to oversimplify (for myself!) there must not have been many students who were really good at English but really bad at Math(s) & vice versa -- often above a certain age level separate (but correlated:) reading & math factors emerge (if enough folks are good at one & bad at the other), but not so in younger groups, b/c they haven't differentiated enough for some to be very good at reading but bad at math/s & vice versa...
ReplyDelete